Communication Networks
We have been focusing on Internet research roughly from 2000 to 2010 or so, working on congestion control, wireless networking, network architecture, resource allocation, topology and routing, network coding, etc. We have developed a mathematical theory of Internet congestion control, developed practical algorithms, built a novel experimental facility (WAN-in-Lab), and transferred our research to the marketplace. Our research FastTCP has been accelerating more than 1TB of Internet traffic every second circa 2014. See the Publications page for the full range of our work. In the following, we highlight some of our results in congestion control.
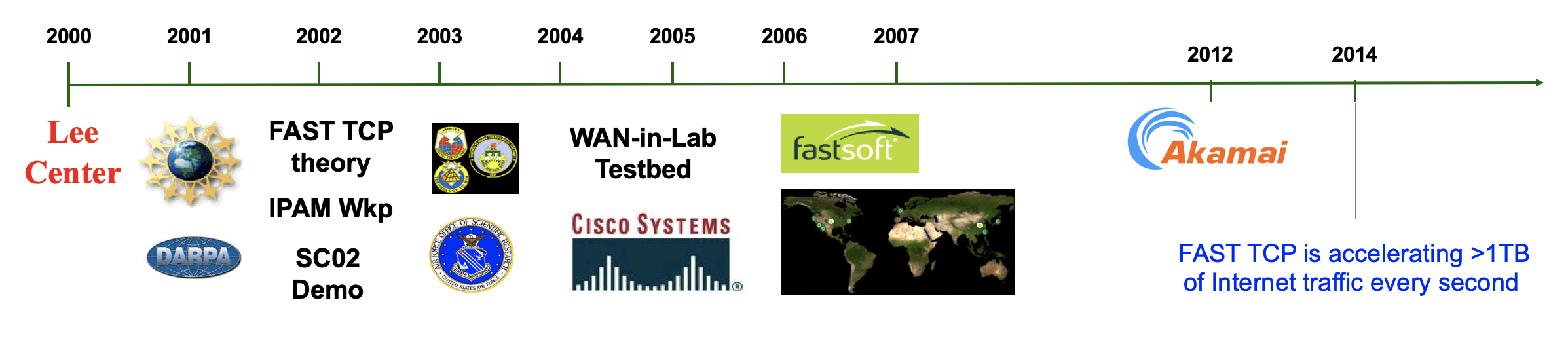
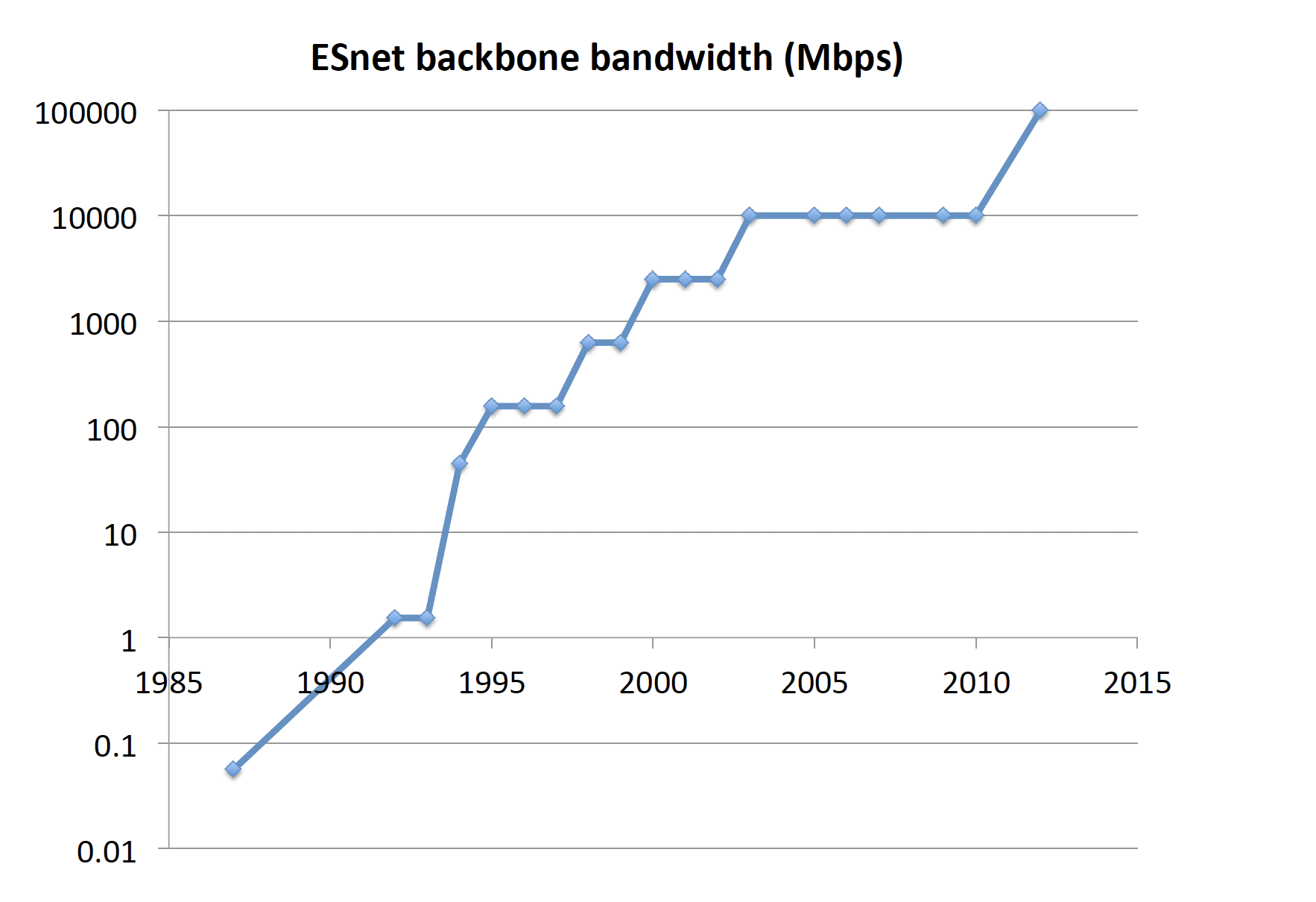
Congestion control has been responsible for maintaining stability as the Internet scaled up in size, speed, traffic volume, coverage, and complexity by many orders of magnitude over the last four decades, especially since late 1980s (see Figure 1). The Internet, called ARPANet at the time, was born in 1969 with four nodes. The Transmission Control Protocol (TCP) was published by Vinton Cert and Robert Kahn in 1974 split into TCP/IP (Transmission Control Protocol/Internet Protocol) in 1978, and deployed as a standard on the ARPANet by 1983. An Internet congestion collapse was detected in October 1986 on a 32 kbps link between the University of California Berkeley campus and the Lawrence Berkeley National Laboratory that is 400 yards away, during which the throughput dropped by a factor of almost 1,000 to 40 bps. Two years later Van Jacobson implemented and published the congestion control algorithm in 1 the Tahoe version of TCP based on an idea of Raj Jain, K.K. Ramakrishnan and Dah-Ming Chiu. Before Tahoe, there were mechanisms in TCP to prevent senders from overwhelming receivers, but no effective mechanism to prevent the senders from overwhelming the network. This was not an issue because there were few hosts, until the mid-1980s. By November 1986 the number of hosts was estimated to have grown to 5,089 but most of the backbone links have remained 50 – 56 bps (bits per second) since the beginning of the ARPANet. Jacobson’s scheme adapts sending rates to the congestion level in the network, thus preventing the senders from overwhelming the network. The algorithm worked very well over a network with relatively low transmission capacity, small delay, and few random packet losses. This was mostly the case in the 1990s, but as the network speed underwent rapid upgrades (see Figure 1), as Internet exploded onto the global scene beyond research and education, and as wireless infrastructure was integrated with and mobile services proliferated on the Internet, the strain on the original design started to show.
This motivated a flurry of research activities on TCP congestion control in the 1990s. A mathematical understanding of Internet congestion control started in the late 1990s with Frank Kelly’s work on network utility maximization. An intensive effort ensued and lasted for a decade, in which we developed a mathematical theory to reverse engineer existing algorithms and understand structural properties of large-scale networks under end-to-end congestion control, systematically designed new algorithms based on analytical insights, and deployed some of these innovations in the field.
A personal account of that effort, focusing on the theory development at Netlab, is summarized in:
- S. H. Low. Analytical methods for network congestion control, ISynthesis Lectures on Communication Networks, Morgan and Claypool Publishers, July 2017
It develops a coherent theory of Internet congestion control from the ground up to help understand and design the equilibrium and stability properties of large-scale networks under end-to-end control. It also demonstrates in depth the entire process of understanding a physical system, building mathematical models of the system, analyzing the models, exploring the practical implications of the analysis, and using the insights to improve a design.
Duality model of congestion control. Our work on congestion control started in the late 1990s at the University of Melbourne, as reported in:
- S. H. Low and D. E. Lapsley. Optimization flow control, I: basic algorithm and convergence, IEEE/ACM Transactions on Networking, 7(6):861-75, Dec 1999
- S. H. Low. A duality model of TCP and queue management algorithms, IEEE/ACM Transactions on Networking, 11(4):525-536, Aug 2003
where we interpret Internet congestion control simply as a gradient projection algorithm carried out by TCP sources and queue management mechanisms over the Internet in real time to solve the dual of a utility maximization problem. It also proves that, provided that the stepsize of the algorithm is small enough, the system will converge even in an asynchronous setting with heterogeneous feedback delays where TCP sources and queue management mechanisms take actions at different times, with different frequencies and using possibly outdated information. This model is applied to understand the delay-based protocol TCP Vegas in:
- S. H. Low, Larry Peterson and Limin Wang. Understanding Vegas: A Duality Model, Journal of ACM, 49(2):207-235, Mar 2002
and has motivated a new active queue management (AQM) algorithm:
- S. Athuraliya, V. H. Li, S. H. Low and Q. Yin. REM: Active Queue Management, IEEE Network, 15(3):48-53, May/Jun 2001
Control theoretic analysis. I then moved to Caltech in 2000 to work with John Doyle and Fernando Paganini to develop a more refined understanding of the impact of feedback delay on the stability properties of TCP algorithms using control theory. An application of this theory to TCP Reno is reported in:
- S. H. Low, F. Paganini, J.Wang and J. C. Doyle. Linear stability of TCP/RED and a Scalable Control, Computer Networks Journal, 43(5):633-647, Dec 2003
that shows that Reno can lose stability when feedback delay increases, or, more strikingly, when link capacity increases. In stark contrast, a scalable TCP/AQM algorithm that maintains linear stability for arbitrary feedback delay and arbitrary link capacity is proposed in:
- F. Paganini, Z.Wang, J. C. Doyle and S. H. Low. Congestion control for high performance, stability and fairness in general networks, IEEE/ACM Transactions on Networking, 13(1):43-56, Feb 2005
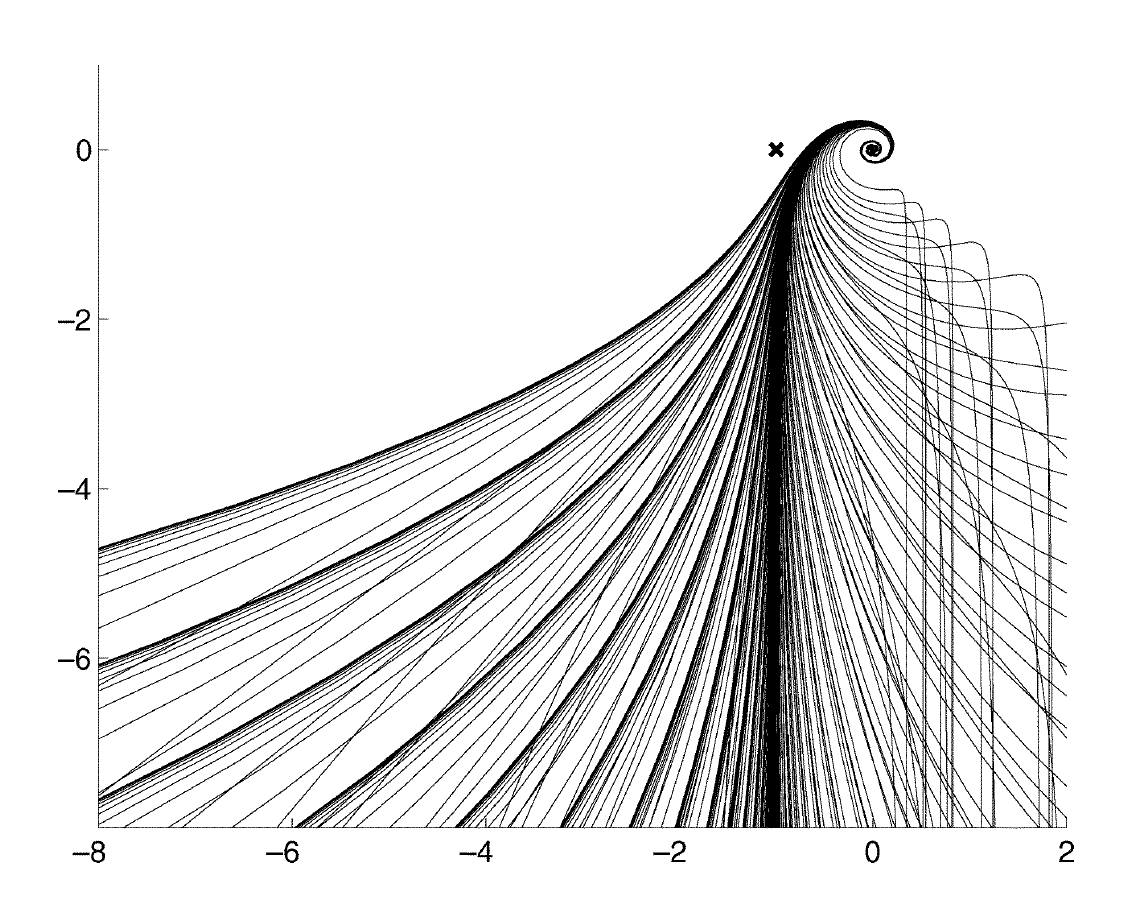
This series of work is summarized in the tutorial:
- S. H. Low, F. Paganini and J. C. Doyle. Internet congestion control, IEEE Control Systems Magazine, 22(1):28-43, Feb 2002
FAST TCP. An important insight from the control-theoretic analysis above is that the dynamics of queueing delay has exactly the right scaling with respect to network capacity. This means that queueing delay as a congestion measure has the distinct advantage of helping maintain stability as a network scales up in capacity, in contrast to the behavior of TCP Reno. This motivates our delay-based FAST TCP protocol for high-speed long-latency networks, reported in:
- David X. Wei, Cheng Jin, Steven H. Low and Sanjay Hegde. FAST TCP: motivation, architecture, algorithms, performance, IIEEE/ACM Transactions on Networking, 14(6):1246-1259, Dec 2006
We started to work with high-energy physics professor Harvey Newman of Caltech in 2002. Our first and stunning demonstration of FAST TCP was Caltech’s first participation in Internet Land Speed Record at SuperComputing Conference in November 2002, organized by Newman and his multi-institution high-energy physics team. The results of the global experiment at SC2002 are reported in:
- C. Jin, D. X. Wei, S. H. Low, G. Buhrmaster, J. Bunn, D. H. Choe, R. L. A. Cottrell, J. C. Doyle, W. Feng, O. Martin, H. Newman, F. Paganini, S. Ravot and S. Singh. FAST TCP: From Theory to Experiments, IEEE Network, IEEE Network, 19(1):4-11, Jan/Feb 2005
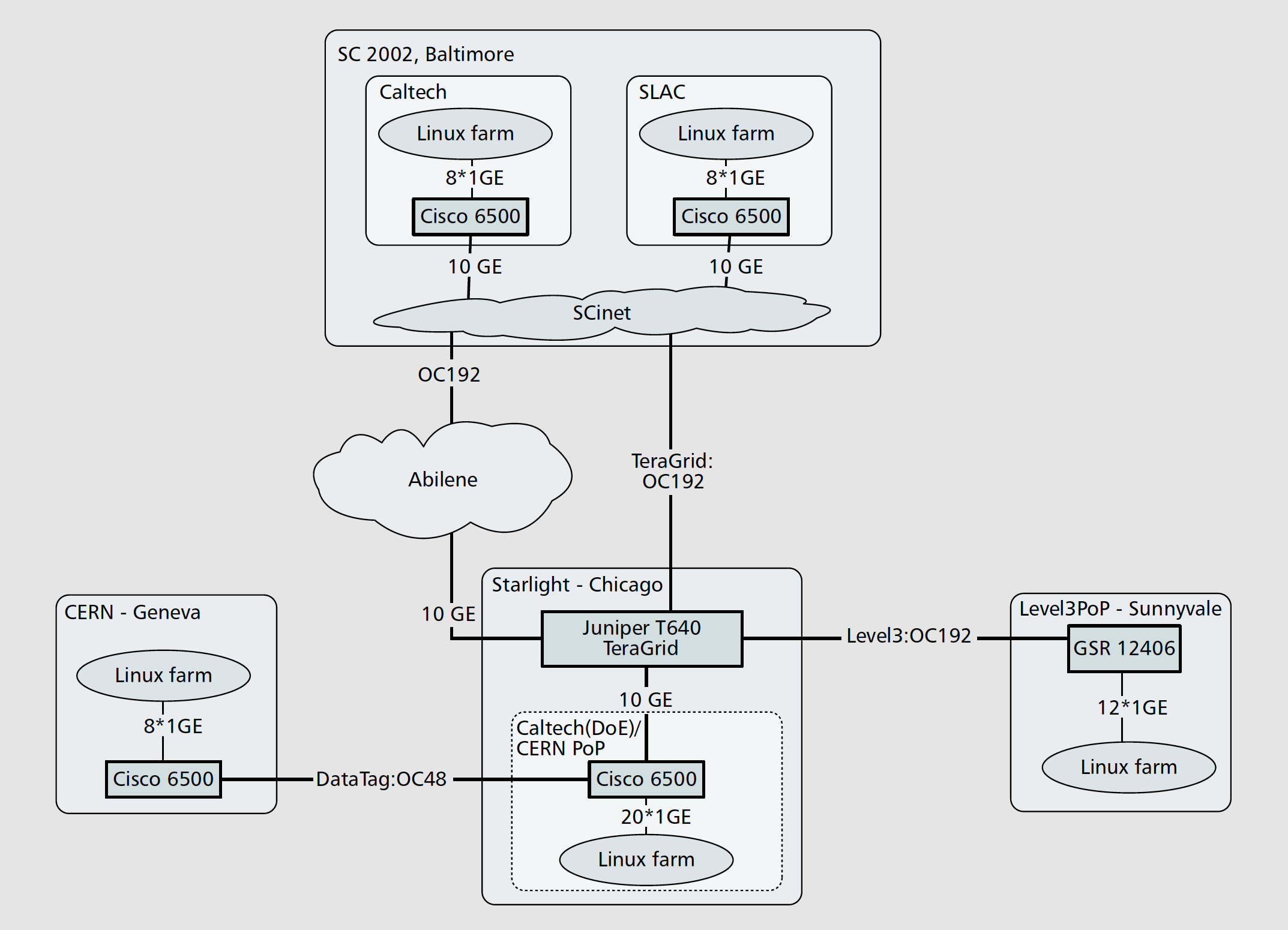
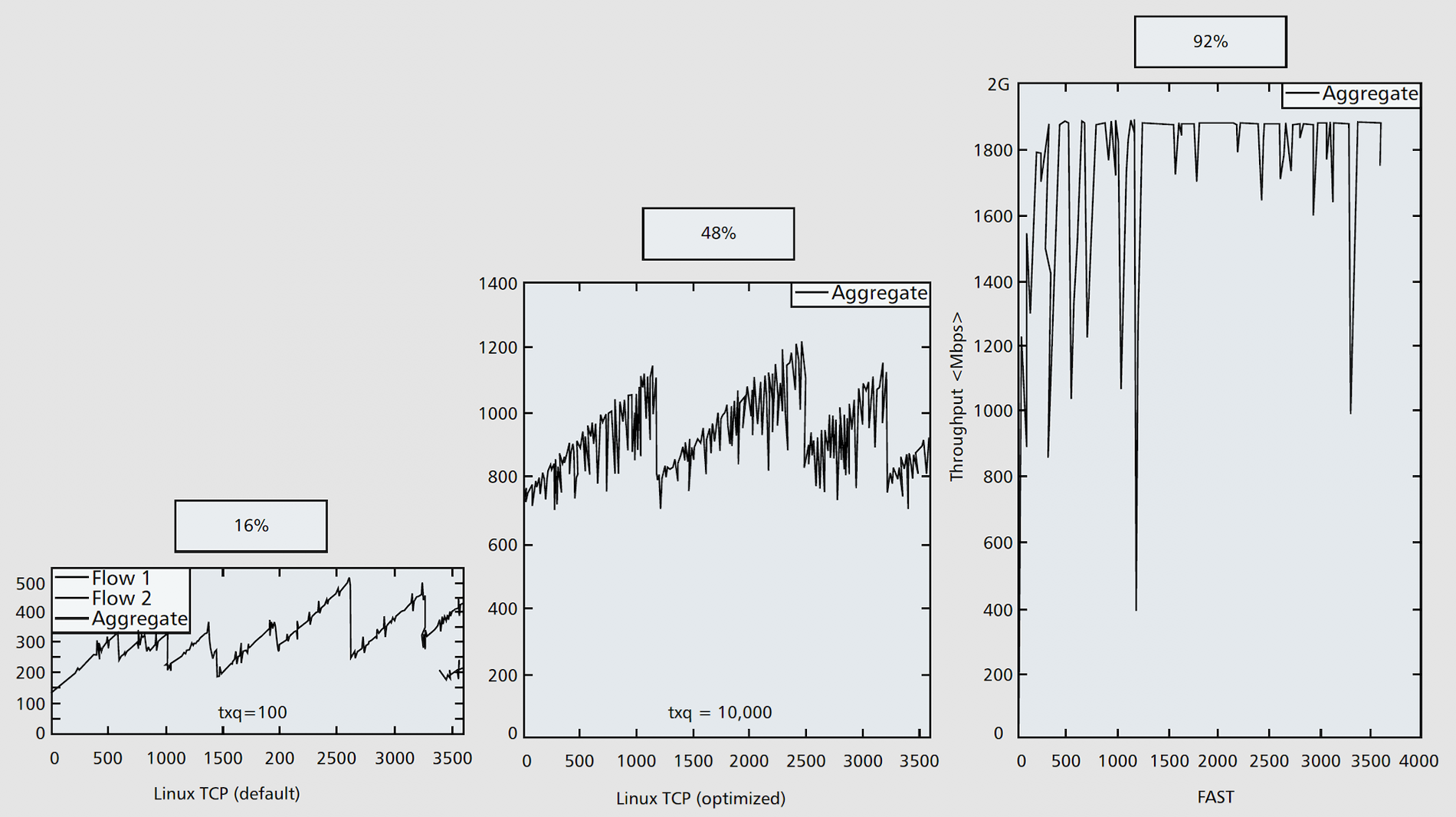
FAST TCP motivated the building of a unique university testbed WAN-in-Lab that used real carrier-class networking hardware to avoid the artifacts introduced by network simulation and emulation, while being localized to allow detailed measurement of network performance:
- George S. Lee, Lachlan L. H. Andrew, Ao Tang and S. H. Low. WAN-in-lab: Motivation, Deployment and Experiments, Proc. Int’l Workshop on Protocols for Fast, Long Distance Networks (PFLDnet), pp. 85-90. Marina Del Rey, CA, 7-9 Feb 2007
Some of us took the effort to deploy our research in the real world through a startup FastSoft. Since 2014, FAST TCP has been accelerating more than 1TB of Internet traffic every second.

TCP/AQM can be interpreted as distributed primal-dual algorithms to maximize aggregate utility over the Internet. In
- J. Wang, L. Li, S. H. Low and J. C. Doyle. Cross-layer optimization in TCP/IP networks, IEEE/ACM Transactions on Networking, 13(3):582-568, Jun 2005
we show that an equilibrium of TCP/IP, if exists, maximizes aggregate utility over both source rates and routes, provided congestion prices are used as link costs. An equilibrium exists if and only if this utility maximization problem and its Lagrangian dual have no duality gap. In this case, TCP/IP incurs no penalty in not splitting traffic across multiple paths.
The vertical decomposition is also observed in wireless networking in
- Lijun Chen, Steven H. Low and John C. Doyle. Joint congestion control and media access control design for wireless ad hoc networks, Proceedings of IEEE Infocom, pp. 2212-2222. Miami, FL, 13-17 Mar 2005
where a utility maximization is decomposed is not only distributed spatially, but also vertically into two protocol layers of TCP and media access control (MAC). This not only provides a systematic way to design and analyze TCP and MAC algorithms, but more importantly, makes their interaction more transparent.
These and other discoveries in the literature suggest a broader model of network architecture that interprets “layering” as “optimization decomposition”, where a network is modeled by a generalized network utility maximization problem, each layer corresponds to a decomposed subproblem, and the interfaces among layers are functions of optimization variables coordinating the subproblems.
- Mung Chiang, S. H. Low, A. Robert Calderbank and John C. Doyle. Layering as optimization decomposition: a mathematical theory of network architectures, Proceedings of the IEEE, vol. 95 pp. 255-312. Jan 2007
A protocol is implemented as a horizontal decomposition into distributed computation and a vertical decomposition into functional modules such as congestion control, routing, scheduling, random access, power control, and channel coding.
The utility maximization model of TCP/AQM equilibrium has counter-intuitive implications analyzed in:
- A. Tang, J. Wang and S. Low. Counter-intuitive throughput behaviors in networks under end-to-end Control, IEEE/ACM Transactions on Networking, 14(2):355-368, Apr 2006
Whereas all examples in the literature suggest that a fair allocation is necessarily inefficient, we characterize exactly the tradeoff between fairness and throughput in general networks. The characterization leads to the first counter-example and trivially explains all the previous supporting examples. Intuitively, we might expect that increasing link capacities always raises aggregate throughput. We show that not only can throughput be reduced when some link increases its capacity, more strikingly, it can also be reduced when all links increase their capacities by the same amount. These examples demonstrate the intricate interactions among sources in a network setting that are missing in a single-link topology that was commonly used in the TCP literature.
When heterogeneous congestion control protocols that react to different pricing signals share the same network, the resulting equilibrium may no longer be interpreted as a solution to the standard utility maximization problem. Nonetheless, we prove the existence of equilibrium in multi-protocol networks in
- Ao Tang, Jintao Wang, S. H. Low and M. Chiang. Equilibrium of heterogeneous congestion control: existence and uniqueness, IEEE/ACM Transactions on Networking, 15(4):824-837, Oct 2007
For almost all networks, the equilibria are locally unique, and finite and odd in number. They cannot all be locally stable unless there is a globally unique equilibrium. We show that if the price mapping functions, which map link prices to effective prices observed by the sources, are sufficiently similar, then global uniqueness is guaranteed.